CODE & DEMO: https://editor.p5js.org/brucexxxbanner/sketches/5uXT2CZaW
———
create a p5js code with canvas all white with 800×400.
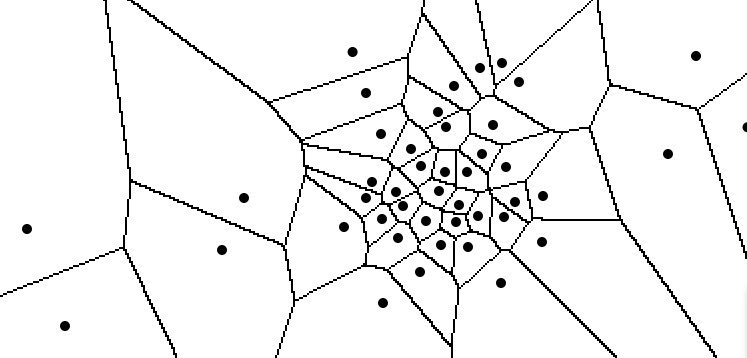
create 21 random draggable nodes on a canvas. add and removeable. simple black dots
create a voronoi diagram prview that uses all nodes on the canvas.
there should be a convex hull around the outer nodes, that should be the outer barrier of the voronoi calcualtion. (like a dynamic mask )
add a button, that generates an SVG diagram on button press.
minimalisitic monochrome CSS. minimalisitic efficent code. no tailwind framework. no title or description in the UI.
📖 THEORIE
Was ein Voronoi-Diagramm ist
Stellen Sie sich vor, Sie streuen eine Handvoll Samenkörner auf einen leeren Boden. Ein Voronoi-Diagramm beantwortet eine einfache Frage: Welcher Bereich des Bodens gehört zu welchem Samenkorn? Jedes Gebiet, auch Zelle genannt, umfasst genau all die Punkte auf dem Boden, die näher an ihrem eigenen Samenkorn liegen als an jedem anderen. Die Grenzen zwischen diesen Gebieten sind immer gerade Linien, die genau in der Mitte zwischen zwei benachbarten Samenkörnern verlaufen. Das Ergebnis ist ein Muster aus vielen polygonischen Zellen, die sich wie eine Art natürliches Puzzle lückenlos aneinanderfügen. Es ist die mathematisch perfekte Art, einen Raum in Einflussbereiche aufzuteilen.
Vorkommen in der Natur und seine Bedeutung
Die Natur ist voller Voronoi-Muster, weil sie oft das Ergebnis effizienter Kräfte ist. Sehen Sie sich eine Giraffenfleckung an, die Haut eines Krokodils oder die zelluläre Struktur eines Blattes an. In allen diesen Fällen wachsen, ziehen sich sich zusammen oder konkurrieren einzelne Einheiten um Platz. Die Girackenflecken entstehen durch Melanin-produzierende Zellen, die während der Embryonalentwicklung wachsen und sich anhalten, wo ihre Einflussbereiche aufeinandertreffen – was genau den Grenzen eines Voronoi-Diagramms entspricht. In einem Bienenwaben-ähnlichen Basaltgestein bewirkt die Abkühlung der Lava, dass sie sich zusammenzieht und an den schwächsten Stellen reißt, die wiederum den mittigen Linien zwischen unsichtbaren Keimzentren folgen. Die tiefere Bedeutung dieses Musters liegt in seiner Optimalität. Es ist eine strukturell stabile und materialsparende Art, eine Fläche zu unterteilen, weshalb die Evolution es so häufig hervorbringt.
Praktische Anwendung in Design und Architektur
Im Design und in der Architektur wird das Voronoi-Diagramm als generatives Werkzeug eingesetzt, um organisch wirkende und hochgradig funktionale Strukturen zu schaffen. Ein Architekt kann es nutzen, um ein filigranes, aber stabiles Deckentragwerk zu entwerfen, bei dem die Dichte der Voronoi-Zellen sich dem Druck von oben anpasst – mehr Struktur, wo mehr Last ist. Ein Designer könnte die Zellen eines Voronoi-Diagramms als Grundrisse für ein variables Parkett verwenden, das natürlich und dynamisch wirkt, anstatt repetitiv. Es findet Anwendung in der Gestaltung von perforierten Fassadenelementen, die Sonnenlicht filtern, oder von Geländern und Möbeln, die Leichtigkeit und Festigkeit vereinen. Der Algorithmus hilft dabei, eine Form zu finden, die sowohl ästhetisch ansprechend als auch den physikalischen Anforderungen optimal angepasst ist.
Der Unterschied zu Delaunay
Während das Voronoi-Diagramm die Gebiete um die Samenkörner herum definiert, konzentriert sich die Delaunay-Triangulierung auf die Verbindungen zwischen ihnen. Wenn Sie im Voronoi-Diagramm alle Samenkörner miteinander verbinden, deren Gebiete eine gemeinsame Grenze haben, erhalten Sie die Delaunay-Triangulierung. Es ist das Skelett, das Netzwerk der Nachbarschaft. Stellen Sie sich das Voronoi-Diagramm als eine politische Landkarte mit Ländergrenzen vor. Die Delaunay-Triangulierung wäre dann die Karte der wichtigsten Autobahnen, die die Hauptstädte dieser Länder miteinander verbinden. Beide beschreiben dieselbe Grundrealität – die Anordnung der Samenkörner –, aber die eine zeigt die Territorien und die andere die Wege, die sie verknüpfen. Sie sind zwei untrennbare Seiten derselben Medaille.
Vorkommen und Bedeutung in Natur, Technik und Wissenschaft
Voronoi-Diagramme kommen in vielen Bereichen vor und sind von großer praktischer und theoretischer Bedeutung. In der Natur finden sie sich beispielsweise in der Struktur von Bienenwaben, wo die Zellen eine annähernd voronoische Form haben, um Platz optimal zu nutzen. In der Geographie werden sie genutzt, um Einzugsgebiete von Städten oder die Verteilung von Ressourcen zu modellieren. In der Technik spielen sie eine Rolle in der Computergrafik, bei der Generierung von natürlichen Texturen, oder in der Robotik für Pfadplanung, wo Roboter den Raum in Regionen einteilen, um Kollisionen zu vermeiden. In der Wissenschaft, insbesondere in der Mathematik und algorithmischen Geometrie, sind Voronoi-Diagramme ein grundlegendes Konzept, das hilft, Probleme der Nähe und Optimierung zu lösen. Ihre Relevanz liegt in der Fähigkeit, komplexe Räume intuitiv und effizient zu strukturieren.
Wechselwirkungen mit anderen natürlichen Strategien und Systemen
Voronoi-Diagramme stehen in engem Verhältnis zu anderen natürlichen Strategien der Raumaufteilung, wie etwa der Tessellation (Parkettierung) oder Selbstorganisation in physikalischen Systemen. Zum Beispiel ähnelt die Bildung von Voronoi-Regionen der Art und Weise, wie Kristalle wachsen oder wie Zellen in biologischem Gewebe angeordnet sind, wo jede Zelle versucht, ihren Platz optimal auszunutzen. Konflikte können auftreten, wenn sich Zentren bewegen oder verändern, was zu dynamischen Anpassungen führt – ähnlich wie bei sich verschiebenden Tierrevieren in der Ökologie. In der Technik konkurrieren Voronoi-basierte Methoden manchmal mit anderen Optimierungsansätzen, wie künstlichen neuronalen Netzen, die ebenfalls Muster erkennen und Räume aufteilen können. Dennoch ergänzen sie sich oft, da Voronoi-Diagramme eine klare, geometrische Grundlage bieten, während andere Systeme mehr Flexibilität bei unscharfen oder sich ändernden Bedingungen haben.
Stellen Sie sich vor, Sie streuen eine Handvoll Samenkörner auf einen leeren Boden. Ein Voronoi-Diagramm beantwortet eine einfache Frage: Welcher Bereich des Bodens gehört zu welchem Samenkorn? Jedes Gebiet, auch Zelle genannt, umfasst genau all die Punkte auf dem Boden, die näher an ihrem eigenen Samenkorn liegen als an jedem anderen. Die Grenzen zwischen diesen Gebieten sind immer gerade Linien, die genau in der Mitte zwischen zwei benachbarten Samenkörnern verlaufen. Das Ergebnis ist ein Muster aus vielen polygonischen Zellen, die sich wie eine Art natürliches Puzzle lückenlos aneinanderfügen. Es ist die mathematisch perfekte Art, einen Raum in Einflussbereiche aufzuteilen.
Vorkommen in der Natur und seine Bedeutung
Die Natur ist voller Voronoi-Muster, weil sie oft das Ergebnis effizienter Kräfte ist. Sehen Sie sich eine Giraffenfleckung an, die Haut eines Krokodils oder die zelluläre Struktur eines Blattes an. In allen diesen Fällen wachsen, ziehen sich sich zusammen oder konkurrieren einzelne Einheiten um Platz. Die Girackenflecken entstehen durch Melanin-produzierende Zellen, die während der Embryonalentwicklung wachsen und sich anhalten, wo ihre Einflussbereiche aufeinandertreffen – was genau den Grenzen eines Voronoi-Diagramms entspricht. In einem Bienenwaben-ähnlichen Basaltgestein bewirkt die Abkühlung der Lava, dass sie sich zusammenzieht und an den schwächsten Stellen reißt, die wiederum den mittigen Linien zwischen unsichtbaren Keimzentren folgen. Die tiefere Bedeutung dieses Musters liegt in seiner Optimalität. Es ist eine strukturell stabile und materialsparende Art, eine Fläche zu unterteilen, weshalb die Evolution es so häufig hervorbringt.
Praktische Anwendung in Design und Architektur
Im Design und in der Architektur wird das Voronoi-Diagramm als generatives Werkzeug eingesetzt, um organisch wirkende und hochgradig funktionale Strukturen zu schaffen. Ein Architekt kann es nutzen, um ein filigranes, aber stabiles Deckentragwerk zu entwerfen, bei dem die Dichte der Voronoi-Zellen sich dem Druck von oben anpasst – mehr Struktur, wo mehr Last ist. Ein Designer könnte die Zellen eines Voronoi-Diagramms als Grundrisse für ein variables Parkett verwenden, das natürlich und dynamisch wirkt, anstatt repetitiv. Es findet Anwendung in der Gestaltung von perforierten Fassadenelementen, die Sonnenlicht filtern, oder von Geländern und Möbeln, die Leichtigkeit und Festigkeit vereinen. Der Algorithmus hilft dabei, eine Form zu finden, die sowohl ästhetisch ansprechend als auch den physikalischen Anforderungen optimal angepasst ist.
Der Unterschied zu Delaunay
Während das Voronoi-Diagramm die Gebiete um die Samenkörner herum definiert, konzentriert sich die Delaunay-Triangulierung auf die Verbindungen zwischen ihnen. Wenn Sie im Voronoi-Diagramm alle Samenkörner miteinander verbinden, deren Gebiete eine gemeinsame Grenze haben, erhalten Sie die Delaunay-Triangulierung. Es ist das Skelett, das Netzwerk der Nachbarschaft. Stellen Sie sich das Voronoi-Diagramm als eine politische Landkarte mit Ländergrenzen vor. Die Delaunay-Triangulierung wäre dann die Karte der wichtigsten Autobahnen, die die Hauptstädte dieser Länder miteinander verbinden. Beide beschreiben dieselbe Grundrealität – die Anordnung der Samenkörner –, aber die eine zeigt die Territorien und die andere die Wege, die sie verknüpfen. Sie sind zwei untrennbare Seiten derselben Medaille.
Vorkommen und Bedeutung in Natur, Technik und Wissenschaft
Voronoi-Diagramme kommen in vielen Bereichen vor und sind von großer praktischer und theoretischer Bedeutung. In der Natur finden sie sich beispielsweise in der Struktur von Bienenwaben, wo die Zellen eine annähernd voronoische Form haben, um Platz optimal zu nutzen. In der Geographie werden sie genutzt, um Einzugsgebiete von Städten oder die Verteilung von Ressourcen zu modellieren. In der Technik spielen sie eine Rolle in der Computergrafik, bei der Generierung von natürlichen Texturen, oder in der Robotik für Pfadplanung, wo Roboter den Raum in Regionen einteilen, um Kollisionen zu vermeiden. In der Wissenschaft, insbesondere in der Mathematik und algorithmischen Geometrie, sind Voronoi-Diagramme ein grundlegendes Konzept, das hilft, Probleme der Nähe und Optimierung zu lösen. Ihre Relevanz liegt in der Fähigkeit, komplexe Räume intuitiv und effizient zu strukturieren.Wechselwirkungen mit anderen natürlichen Strategien und Systemen
Voronoi-Diagramme stehen in engem Verhältnis zu anderen natürlichen Strategien der Raumaufteilung, wie etwa der Tessellation (Parkettierung) oder Selbstorganisation in physikalischen Systemen. Zum Beispiel ähnelt die Bildung von Voronoi-Regionen der Art und Weise, wie Kristalle wachsen oder wie Zellen in biologischem Gewebe angeordnet sind, wo jede Zelle versucht, ihren Platz optimal auszunutzen. Konflikte können auftreten, wenn sich Zentren bewegen oder verändern, was zu dynamischen Anpassungen führt – ähnlich wie bei sich verschiebenden Tierrevieren in der Ökologie. In der Technik konkurrieren Voronoi-basierte Methoden manchmal mit anderen Optimierungsansätzen, wie künstlichen neuronalen Netzen, die ebenfalls Muster erkennen und Räume aufteilen können. Dennoch ergänzen sie sich oft, da Voronoi-Diagramme eine klare, geometrische Grundlage bieten, während andere Systeme mehr Flexibilität bei unscharfen oder sich ändernden Bedingungen haben.