Delaunay-Triangulierungen, und generative Origami hafte Faltungen sprechen eine gemeinsame Sprache sprechen: die Sprache der strukturell effizienten Geometrie. Die Delaunay-Triangulierung ist ein mathematisches Verfahren, das eine Punktwolke in ein Netzwerk von Dreiecken zerlegt, die sich durch ihre maximale Gleichseitigkeit und minimale Anzahl von „schmalen“ Dreiecken auszeichnen. Genau diese Eigenschaften sind für stabiles und vorhersagbares Falten entscheidend.
Im Origami dienen Falten, die ein Dreiecksmuster (ein Triangulationsmuster) bilden, dazu, flache Blätter in stabile, komplexe 3D-Formen zu überführen. Jedes Dreieck ist eine starre, aber kippbare Einheit. Die Delaunay-Triangulierung liefert die ideale Grundlage für solche Faltmuster, da sie die mechanisch robusteste und mathematisch eleganteste Aufteilung der Fläche bietet. Sie minimiert interne Spannungen und sorgt für eine gleichmäßige Kraftverteilung.
basic delaunay folding
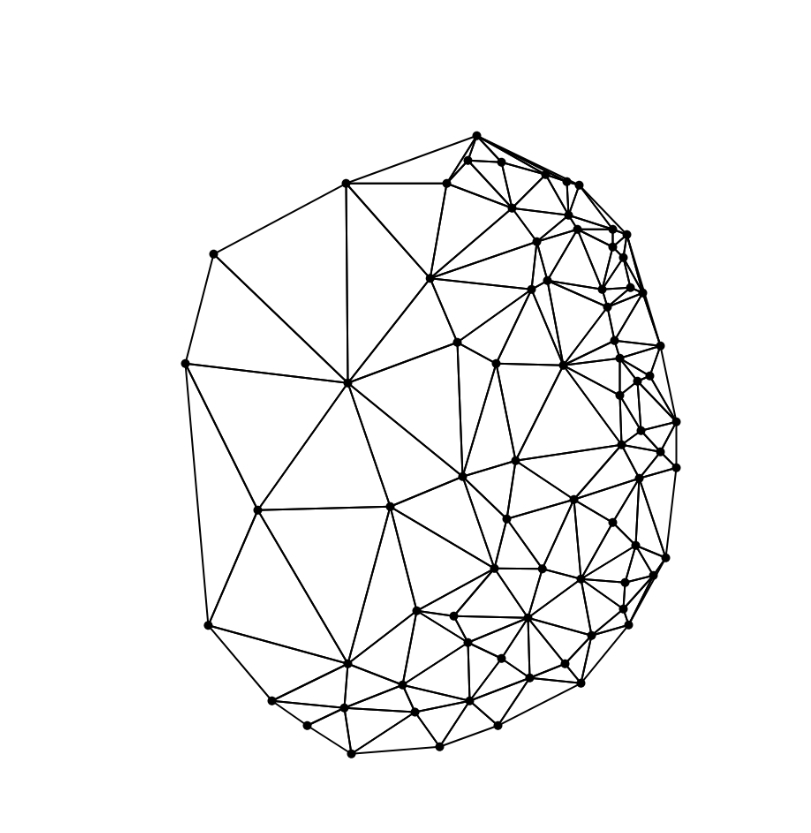
DEMO & CODE https://editor.p5js.org/brucexxxbanner/sketches/CMsFfmnTI
basic delaunay folding with interpolated greyscale map

DEMO & CODE: https://editor.p5js.org/brucexxxbanner/sketches/xs3ZcxYH3
basic delaunay with custom hull contour

DEMO & CODE: https://editor.p5js.org/brucexxxbanner/sketches/OW0XFPq8c